sellingtrio.blogg.se - Difference equation systems

#Difference equation systems software
#Difference equation systems series

"On an electrodynamic origin of quantum fluctuations". Delay Differential Equations with Applications in Population Dynamics. Dordrecht, NL: Kluwer Academic Publishers. Stability and Oscillations in Delay Differential Equations of Population Dynamics. Nonlinear Analysis: Real World Applications. "Construction of Lyapunov functionals for delay differential equations in virology and epidemiology". ^ Kajiwara, Tsuyoshi Sasaki, Toru Takeuchi, Yasuhiro ()."Mathematical Model for the Epidemiology of Tuberculosis, with Estimates of the Reproductive Number and Infection-Delay Function". Selected Papers, The Third International Conference on the Numerical Solutions of Volterra and Delay Equations.

#Difference equation systems software

"Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview".

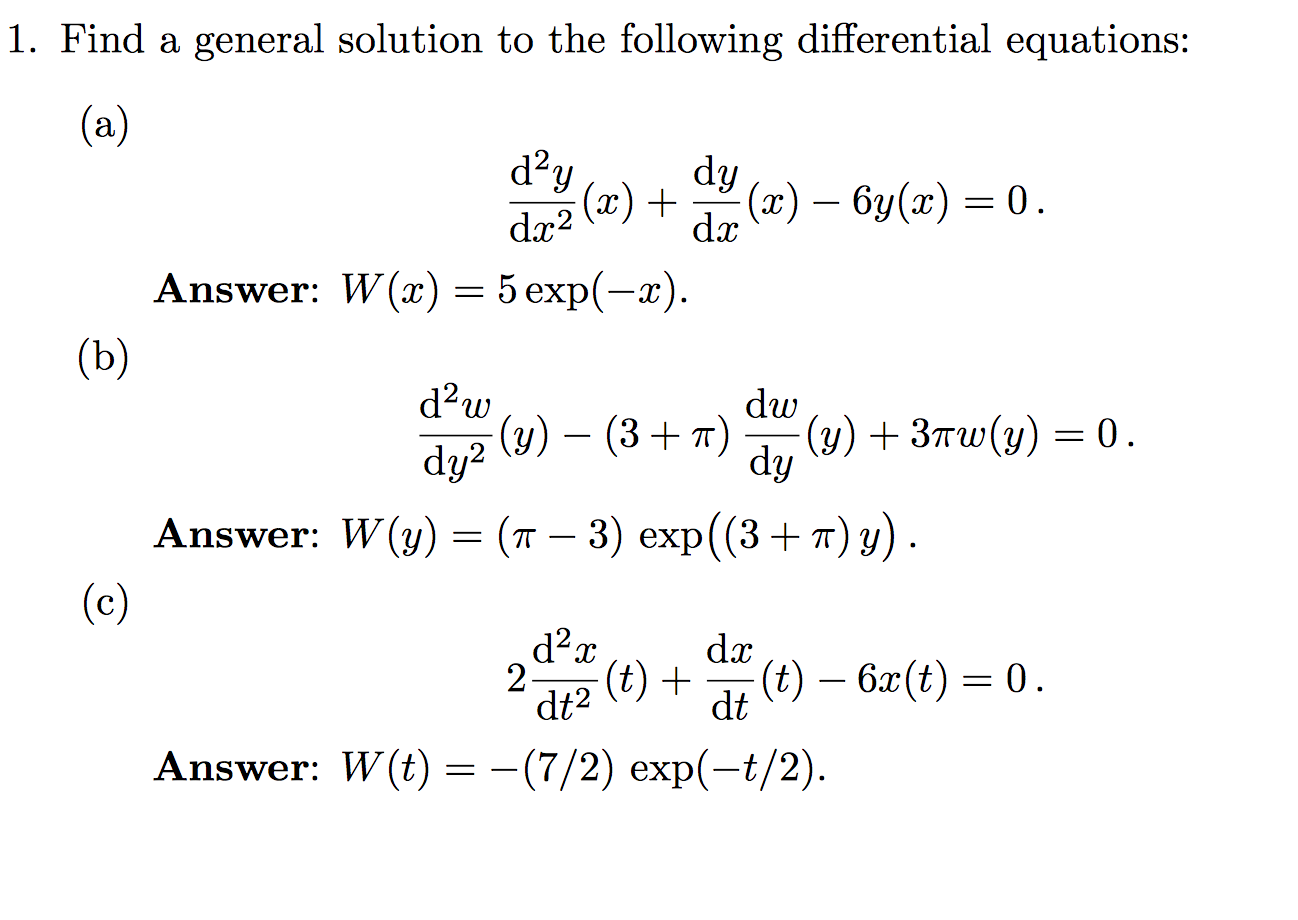
^ Makroglou, Athena Li, Jiaxu Kuang, Yang ().Society for Industrial and Applied Mathematics. Stability and Stabilization of Time-Delay Systems. ^ Michiels, Wim Niculescu, Silviu-Iulian (2007).

#Difference equation systems series

Series A, Mathematical and Physical Sciences. Proceedings of the Royal Society of London. "The dynamics of a current collection system for an electric locomotive". "The pantograph equation in quantum calculus". Proceedings of the 2010 American Control Conference: 5781–5788. "Simple delay-based implementation of continuous-time controllers". ^ Lavaei, Javad Sojoudi, Somayeh Murray, Richard M."Time Delay Systems: An overview of some recent advances and open problems". Consider, for example, the following DDE: In some special situations it is possible to solve the characteristic equation explicitly. This characteristic equation is a nonlinear eigenproblem and there are many methods to compute the spectrum numerically. For instance, even though there are an infinite number of eigenvalues, there are only a finite number of eigenvalues to the right of any vertical line in the complex plane. The spectrum does however have some properties which can be exploited in the analysis. Because of the exponential in the characteristic equation, the DDE has, unlike the ODE case, an infinite number of eigenvalues, making a spectral analysis more involved. The roots λ of the characteristic equation are called characteristic roots or eigenvalues and the solution set is often referred to as the spectrum.

In spite of their complexity, DDEs often appear as simple infinite-dimensional models in the very complex area of partial differential equations (PDEs).Ī general form of the time-delay differential equation for x ( t ) ∈ R n.

Voluntary introduction of delays can benefit the control system.

In worst cases (time-varying delays, for instance), it is potentially disastrous in terms of stability and oscillations. Unfortunately, ignoring effects which are adequately represented by DDEs is not a general alternative: in the best situation (constant and known delays), it leads to the same degree of complexity in the control design.

Delay systems are still resistant to many classical controllers: one could think that the simplest approach would consist in replacing them by some finite-dimensional approximations.

Then, the interest for DDEs keeps on growing in all scientific areas and, especially, in control engineering. Finally, besides actual delays, time lags are frequently used to simplify very high order models. In addition, actuators, sensors, and communication networks that are now involved in feedback control loops introduce such delays. Many processes include aftereffect phenomena in their inner dynamics.

Aftereffect is an applied problem: it is well known that, together with the increasing expectations of dynamic performances, engineers need their models to behave more like the real process.

Four points may give a possible explanation of the popularity of DDEs: partial differential equations (PDEs) which are infinite dimensional, as opposed to ordinary differential equations (ODEs) having a finite dimensional state vector.

They belong to the class of systems with the functional state, i.e. In mathematics, delay differential equations ( DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times.ĭDEs are also called time-delay systems, systems with aftereffect or dead-time, hereditary systems, equations with deviating argument, or differential-difference equations.